Τα θέματα και οι προτεινόμενες λύσεις των Μαθηματικών από το φροντιστήριο "ΚΥΚΛΟΣ"

ΘΕΜΑ Α 

Α1. Έστω η συνάρτηση f(x) = x²για κάθε x ∈ ℝ. Να αποδείξετε ότι  f^′(x) = 2x. 

Μονάδες 7 

Α2. Να δώσετε τον ορισμό της διαμέσου (δ) ενός δείγματος ν  παρατηρήσεων. 

Μονάδες 6 

Α3. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν,  γράφοντας στο τετράδιό σας, δίπλα στο γράμμα που  αντιστοιχεί σε κάθε πρόταση, τη λέξη Σωστό, αν η πρόταση  είναι σωστή, ή τη λέξη Λάθος, αν η πρόταση είναι  λανθασμένη. 

α. Ο συντελεστής μεταβολής δεν είναι ανεξάρτητος από τις  μονάδες μέτρησης. 

β. Αν μία συνάρτηση f είναι παραγωγίσιμη σε ένα διάστημα Δ και ισχύει f^′(x) > 0 για κάθε εσωτερικό σημείο του Δ, τότε  η f είναι γνησίως αύξουσα στο Δ. 

γ. Ο σταθμικός μέσος είναι μέτρο διασποράς. 

Μονάδες 6 

Α4. Να μεταφέρετε στο τετράδιό σας τις παρακάτω ελλιπείς ισότητες και να τις συμπληρώσετε σωστά: 

α. (√x)^′= ⋯ 

β. (f(g(x)))^′ = ⋯ 

Μονάδες 6

ΤΕΛΟΣ 1ΗΣ ΑΠΟ 4 ΣΕΛΙΔΕΣ 

ΑΡΧΗ 2ΗΣ ΣΕΛΙΔΑΣ 

ΘΕΜΑ Β 

Κατά τον μήνα Νοέμβριο οι απουσίες πέντε (5) μαθητών ήταν:  25, 10, 5, 20, 15. 

Β1. Να υπολογίσετε τη μέση τιμή x̅ (μον.4) και το εύρος (μον. 3)  του παραπάνω δείγματος των πέντε μαθητών. 

Μονάδες 7 

Β2. Να υπολογίσετε τη διακύμανση s². 

Μονάδες 7 

Β3. Να υπολογίσετε τον συντελεστή μεταβολής CV του  δείγματος (μον. 6) και να εξετάσετε αν το δείγμα είναι  ομοιογενές απαντώντας αιτιολογημένα (μον. 5). 

Μονάδες 11 

ΘΕΜΑ Γ 

Δίνεται η συνάρτηση f(x) = x³ − 9x² + αx + 1, όπου x, α ∈ ℝ. 

Γ1. Αν ο ρυθμός μεταβολής της f για x = 1 είναι ίσος με 0, να  δείξετε ότι α = 15. 

Μονάδες 6  

Γ2. Για α = 15 να βρείτε την εξίσωση της εφαπτομένης της  γραφικής παράστασης της f στο σημείο Μ(2, f(2)). 

Μονάδες 6 

Γ3. Για α = 15 να μελετήσετε τη συνάρτηση f(x) ως προς τη  μονοτονία (μον. 6) και τα ακρότατα (μον. 2). 

Μονάδες 8  

Γ4. Για α = 15 να βρείτε το όριο 

lim x→1 

f^′(x) 

x² − 1 

Μονάδες 5

ΤΕΛΟΣ 2ΗΣ ΑΠΟ 4 ΣΕΛΙΔΕΣ 

ΑΡΧΗ 3ΗΣ ΣΕΛΙΔΑΣ 

ΘΕΜΑ Δ 

Δίνεται η συνάρτηση  

f(x) ₌x 

x + 1 

Δ1. Να βρεθεί το πεδίο ορισμού της συνάρτησης (μον. 2) και να  υπολογίσετε την παράγωγο f^′(x) (μον. 4). 

Μονάδες 6 

Δ2. Υποθέτουμε ότι ο χρόνος επιστροφής , σε λεπτά, από το  σχολείο στο σπίτι για τους μαθητές μίας περιφέρειας  ακολουθεί την κανονική κατανομή, με μέση τιμή και τυπική  απόκλιση  

x̅ =¹ 

f^′(2₎, s =¹ 

2f ^′(1) 

αντίστοιχα. 

Να δείξετε ότι x̅ = 9 και s = 2. 

Μονάδες 6 

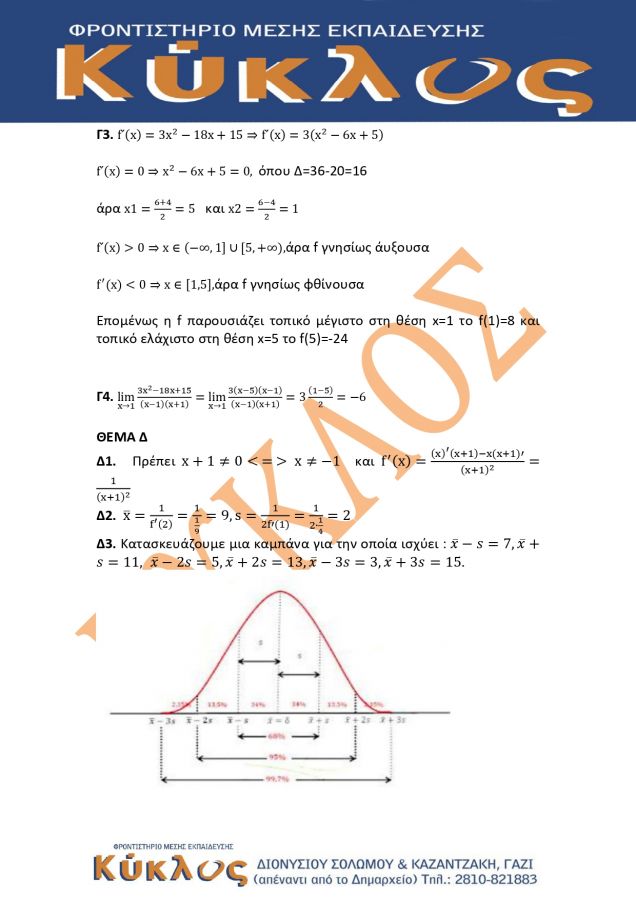
Δ3. Αν το πλήθος των μαθητών της περιφέρειας είναι 2000, πόσοι από αυτούς έχουν χρόνο επιστροφής από 5 έως 11 λεπτά (μον. 6) και πόσοι πάνω από 15 λεπτά (μον. 3); 

Μονάδες 9 

Δ4. Να υπολογίσετε τη μέση τιμή και την τυπική απόκλιση, στην  περίπτωση που ο χρόνος επιστροφής των μαθητών της  περιφέρειας αυξηθεί κατά 3 λεπτά. 

Μονάδες 4

Σχολιασμός Θεμάτων

"Πρόκειται για θέματα που καλύπτουν όλο το εύρος της ύλης και το πλεονέκτημα τους είναι πως χαρακτηρίζονται ως διαβαθμισμένης δυσκολίας δίνοντας την ευκαιρία στον μαθητή να γράψει. Το θέμα Α και Β χαρακτηρίζονται βατά. H μεθοδολογία στο θέμα Γ είναι γνωστή, χρειαζόταν προσοχή στις πράξεις. Το θέμα Δ ήταν για καλά προετοιμασμένους μαθητές στο κομμάτι της στατιστικής."

Δασκαλάκη Μαρία-Όλγα

Δασκαλάκη Δήμητρα

Μαθηματικοί του φροντιστηρίου ''ΚΥΚΛΟΣ''